Hauptnavigation

General

Research

Teaching

Staff

ID3 next up previous contents
Weiter: C4.5 und J4.8 Hoch: Lernalgorithmen Zurück: Lernalgorithmen


ID3

Der ID3 Algorithmus [QUINLAN 1983] ist ein klassisches induktives Lernverfahren. Es konstruiert nach dem top-down-Prinzip einen Entscheidungsbaum, indem aus Beispielen mit Hilfe von statistischer Merkmalsselektion gelernt wird.

Ein Entscheidungsbaum hat Kanten, an denen Attributwerte stehen, Konten sind Verzweigungspunkte und Bl?tter stellen Klassifikationen dar. Um zu entscheiden, ob ein neues Beispiel zu einer Klasse geh?rt, wird den Kanten gefolgt, deren Beschriftung einem Attributwert des Beispiels entspricht, bis ein Blatt erreicht ist [MORIK 1995]. Eine der wesentlichen Eigenschaften der Klassifikation ist dabei die Diskretisierung. D.h. die einzelnen Klassen sind scharf von einander getrennt, so dass ein Fall, bestehend aus einzelnen Werten, entweder zu einer Klasse geh?rt oder nicht.

Um einen Entscheidungsbaum aufzubauen, muss der Algorithmus f?r jeden Konten berechnen, welches Attribut ihm zugewiesen wird. Dies ist das zentrale Auswahlproblem von ID3. Es muss entschieden werden, welches Attribut den gr??ten Informationsgewinn bringt, um die Trainingsdaten bestm?glich zu klassifizieren. Ist das Problem gel?st, wird das Attribut ausgew?hlt und f?r jeden m?glichen Wert des Attributs wird eine Kante mit Kindknoten erzeugt. Das ausgew?hlte Attribut kann nun aus der Liste aller Attribute entfernt werden. Die Kindknoten werden weiter nach dem gleichen Schema rekursiv unterteilt, bis in den Knoten nur noch Objekte einer Klasse stehen. Diese Knoten bilden die Bl?tter des Baumes, welche die Klassenkennzeichnung des entsprechenden Objektes enthalten.

Der Informationsgehalt eines Attributs st?tzt sich auf die, aus der Informationstheorie stammenden Gr??e, Entropie. Sie berechnet sich nach [MORIK 1995] mit der Formel:

- $\displaystyle \sum_{m=1}^{n}$pmlog2pm

wobei n f?r die Anzahl der Attributwerte steht und pm die Wahrscheinlichkeit, des Vorkommens des Zielattributs, mit dem Index m, in der Trainingsdatenmenge, angibt.

Der Informationsgewinn eines Attributs ergibt sich durch den Vergleich24 der Entropie des Attributs mit der Entropie der Trainingsmenge. So ist es m?glich das Attribut mit dem gr??ten Informationsgehalt zu bestimmen und auszuw?hlen.

Der Aufbau eines optimalen Entscheidungsbaumes ist nach [HYAFIL . RIVEST 1976] NP-vollst?ndig, d.h. das Problem kann nicht mit Hilfe eines deterministischen Algorithmuses in polynomineller Laufzeit berechnet werden. Der ID3 Algorithmus benutzt einen nonbacktracking greedy Algorithmus, was bedeutet, dass das zu w?hlende Attribut immer auf der Basis des momentanen Wissenstands bestimmt wird. Auch wenn sich sp?ter vielleicht herausstellen w?rde, dass die Wahl eines anderen Attributes g?nstiger gewesen w?re.

Zur Illustration des Algorithmuses wird als n?chstes, an einem kleinen Beispiel, ein Entscheidungsbaum hergeleitet [MITCHELL 1997]. Die Tabelle 6.1 beschreibt, ob es an bestimmten Samstagmorgenden m?glich war, Tennis zu spielen oder nicht.


Tabelle 6.1: War Tennisspielen samstagmorgens m?glich?
Nummer Aussicht Temperatur Luftfeuchtigkeit Wind Tennis spielen?  
1 sonnig hei? hoch nein negativ  
2 sonnig hei? hoch ja negativ  
3 bew?lkt hei? hoch nein positiv  
4 Regen mild hoch nein positiv  
5 Regen kalt normal nein positiv  
6 Regen kalt normal ja negativ  
7 bew?lkt kalt normal ja positiv  
8 sonnig mild hoch nein negativ  
9 sonnig kalt normal nein positiv  
10 Regen mild normal nein positiv  
11 sonnig mild normal ja positiv  
12 bew?lkt mild hoch ja positiv  
13 bew?lkt hei? normal nein positiv  
14 Regen mild hoch ja negativ  


Um die Entropie der Beispielmenge zu berechnen, betrachtet man die Spalte »Tennis spielen?« (Zielattribut).

$ {\frac{9}{14}}$log2$ {\frac{9}{14}}$ = - 0, 4098 f?r positive Beispiele
$ {\frac{5}{14}}$log2$ {\frac{5}{14}}$ = - 0, 5305 f?r negative Beispiele
Entropie der Beispielmenge = - (- 0, 4098 - 0, 5305) =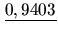 $ \underline{0,9403}$

Berechnung der Entropie f?r Aussicht:
sonnig:
$ {\frac{2}{5}}$log2$ {\frac{2}{5}}$ = - 0, 5288 f?r positive Beispiele
$ {\frac{3}{5}}$log2$ {\frac{3}{5}}$ = - 0, 4422 f?r negative Beispiele
Summe mit umgekehrtem Vorzeichen: 0, 971


bew?lkt:
$ {\frac{4}{4}}$log2$ {\frac{4}{4}}$ = 0 f?r die vier positiven Beispiele
Regen:
$ {\frac{3}{5}}$log2$ {\frac{3}{5}}$ = - 0, 5288 f?r positive Beispiele
$ {\frac{2}{5}}$log2$ {\frac{2}{5}}$ = - 0, 4422 f?r negative Beispiele
Summe mit umgekehrtem Vorzeichen: 0, 971


Entropie f?r Aussicht: $ {\frac{9}{14}}$ . 0, 971 + $ {\frac{9}{14}}$ . 0 + $ {\frac{9}{14}}$ . 0, 971 = $ \underline{0,6935}$
Der Informationsgewinn durch dieses Attribut ergibt sich aus dem Vergleich mit der Entropie der Beispielmenge:
0, 9403 - 0, 6935 = $ \underline{\underline{0,247}}$

Die Informationsgewinne der anderen drei Attribute berechnen sich analog:

Informationsgewinn (Temperatur) = 0,029
Informationsgewinn (Luftfeuchtigkeit) = 0,151
Informationsgewinn (Wind) = 0,048

Die Berechnungen des Informationsgewinns der einzelnen Attribute zeigen, dass das Attribut Aussicht am Besten geeignet ist um die Daten zu ordnen. Wenn Aussicht ausgew?hlt wurde, werden drei Kanten angelegt und mit sonnig, bew?lkt und Regen beschriftet. Der unter bew?lkt gebildete Knoten enth?lt nur positiv klassifizierte Beispiele und wird damit zum Blatt (siehe Abbildung 6.1).

Abbildung 6.1: halbfertiger Entscheidungsbaum
\begin{figure}\centering\epsfig{file=bilder/teilbaum.eps, width=13cm} \end{figure}

Der unter sonnig und Regen gebildete Knoten muss genau wie der oberste behandelt werden. Am Ende ergibt sich der in Abbildung 6.2 abgebildete Entscheidungsbaum.

Abbildung 6.2: fertiger Entscheidungsbaum
\begin{figure}\centering\epsfig{file=bilder/baum.eps, width=14.7cm} \end{figure}

next up previous contents
Weiter: C4.5 und J4.8 Hoch: Lernalgorithmen Zurück: Lernalgorithmen
Christian H?ppe, christian.hueppe@web.de