| Description |
The learning task is to revise a given theory, in order to no longer imply a given set of unwanted facts.
In other words, a theory has become inconsistent and shall be adjusted to some new insights.
An obvious demand is, that adjustment should not change more of the theory than necessary. In particular, parts
that are not concerned in the derivation of the incorrect logical facts should not be changed at all.
|
| Definition |
Given are
- a theory B, described in first order logic, and
- a set F of logical facts.
The task is to find a revision of B, that is a maximally general
correct specialization of B with respect to F, denoted
rev(B, F).
Rev is a general correct specialization operator, if and only if the following constraints
hold for all theories B and set of facts F :
- Cn(rev(B, F)) ∩ F = ∅,
- Cn(rev(B, F)) ⊆ Cn(B)
- For all theories B' : Cn(rev(B, F)) ⊂ Cn(B')
⊆ Cn(B) ⇒ Cn(B') ∩ F ≠ ∅.
Cn(S) denotes the set of all formulas, implied by S.
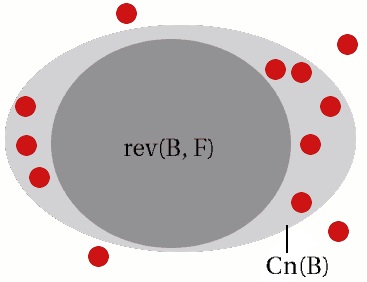
In the picture above,
- the outer circle represents a theory B with all of its
consequences.
- The red dots represent statements, that turned out to be wrong,
so they should not be part of the theory or its consequences.
For some of the red dots lay in the outer circle, we need to find
another theory/circle.
- The darker gray circle lays within the outer circle, but it does
not contain any red dot. This makes it a candidate for a revision.
There is another constraint, which has to be met:
The candidate has to be most general.
For instance there mustn't be another circle,
- laying in the outer circle,
- containing the dark gray circle,
- and not containing a red dot,
because otherwise this circle would be a better revision.
|

